Measuring Association

Sociology 312/412/512, University of Oregon

Aaron Gullickson

Thinking about association

The primary goal of most social science statistical analysis is to establish whether there is an association between variables and to describe the strength and direction of this association.

  • Is income inequality in a country related to life expectancy?
  • Do stronger networks predict better success at finding jobs for job seekers?
  • Does population size and growth predict environmental degradation?
  • How does class affect party affiliation and voting?

Association vs. causation

We often think about the relationships we observe in data as being causally determined, but the simple measurement of association is insufficient to establish a necessary causal connection between the variables.

Spuriousness

The association between two variables could be generated because they are both related to a third variable that is actually the cause.

Reverse causality

We may think that one variable causes the other, but it is equally possible that the causal relationship is the other way.

Different methods for measuring association

Two categorical variables

The two-way table and comparative barplots

Categorical and quantitative variable

Mean differences and comparative boxplots

Two quantitative variables

The correlation coefficient and scatterplots

The Two-Way Table

The two-way table

The two-way table (or cross-tabulation) gives the joint distribution of two categorical variables.

We can create a two-way table in R using the table command but this time we feed in two different variables. Here is an example using sex and survival on the titanic:

tab <- table(titanic$sex, titanic$survival)
tab
        
         Survived Died
  Female      339  127
  Male        161  682

There were 339 female survivors, 127 female deaths, and so on.

Raw numbers are never enough

Sex Survived Died
Female 339 127
Male 161 682
  • It might seem like the much higher number of male deaths is enough to claim that there is a relationship between gender and survival, but this comparison would be flawed. Why?
  • There were a lot more male passengers on the Titanic than female passengers. So even if they had the same probability of survival, we would expect to see more male deaths.
  • We need to compare the proportion of deaths among men to the proportion of deaths among women to make a proper comparison.
  • Never, ever compare raw numbers directly. Instead, we need to first calculate a conditional distribution using proportions. In this case, I want the distribution of survival conditional on gender.

Calculate maginal distributions

A first step in establishing the relationship is to calculate the marginal distributions of the row and column variables. The marginal distributions are simply the distributions of each categorical variable separately. We can calculate these from the tab object I created using the margin.table command in R:

margin.table(tab, 1)

Female   Male 
   466    843 
margin.table(tab, 2)

Survived     Died 
     500      809

Note that the the option 1 here gives me the row marginal and the option 2 gives me the column marginal.

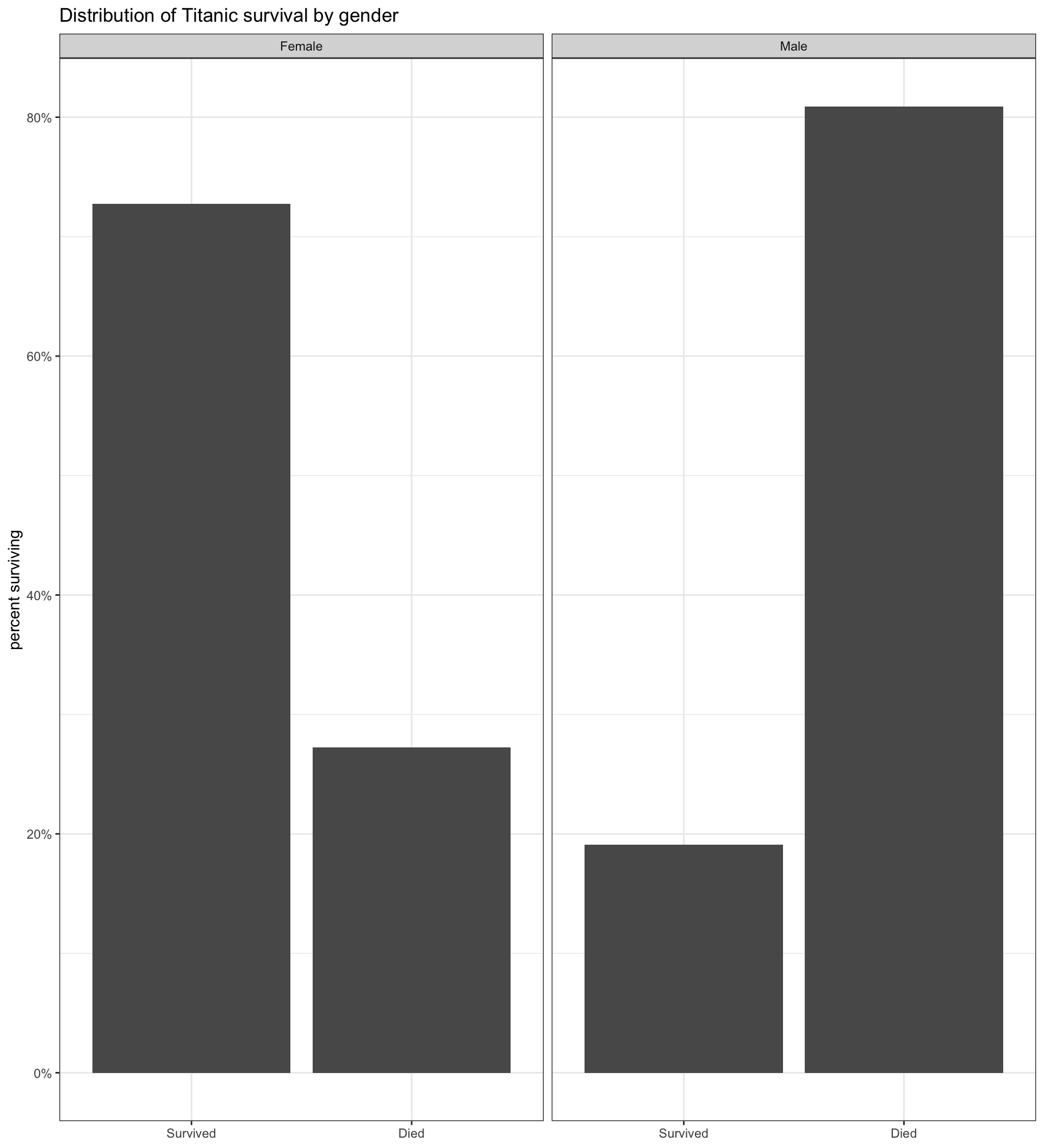
Distribution of survival conditional on sex

Sex Survived Died Total
Female 339 127 466
Male 161 682 843
Total 500 809 1309

To get distribution of survival by gender, divide each row by row totals:

Sex Survived Died Total
Female 339/466 127/466 466
Male 161/843 682/843 843
Sex Survived Died Total
Female 0.727 0.273 1.0
Male 0.191 0.809 1.0
  • Read the distribution within the rows:
    • 72.7% of women survived and 27.3% of women died.
    • 19.1% of men survived and 80.9% of men died.
  • Men were much more likely to die on the Titanic than women.

Calculating conditional distributions in R

You can use prop.table to calculate conditional distributions in R.

tab <- table(titanic$sex, titanic$survival)
prop.table(tab, 1)
        
          Survived      Died
  Female 0.7274678 0.2725322
  Male   0.1909846 0.8090154
  • Take note of the 1 as the second argument in prop.table. You must include this to get the distribution of the column variable conditional on the row.
  • Make sure that the proportions sum up to one within the rows to check yourself.

The other conditional distribution

prop.table(tab, 2)
        
          Survived      Died
  Female 0.6780000 0.1569839
  Male   0.3220000 0.8430161

What changed?

  • Notice that the rows do not sum to one anymore. However, the columns do sum to one.
  • Because of the 2 in the prop.table command, we are now looking at the distribution of gender conditional on survival.

Comparative barplot by faceting

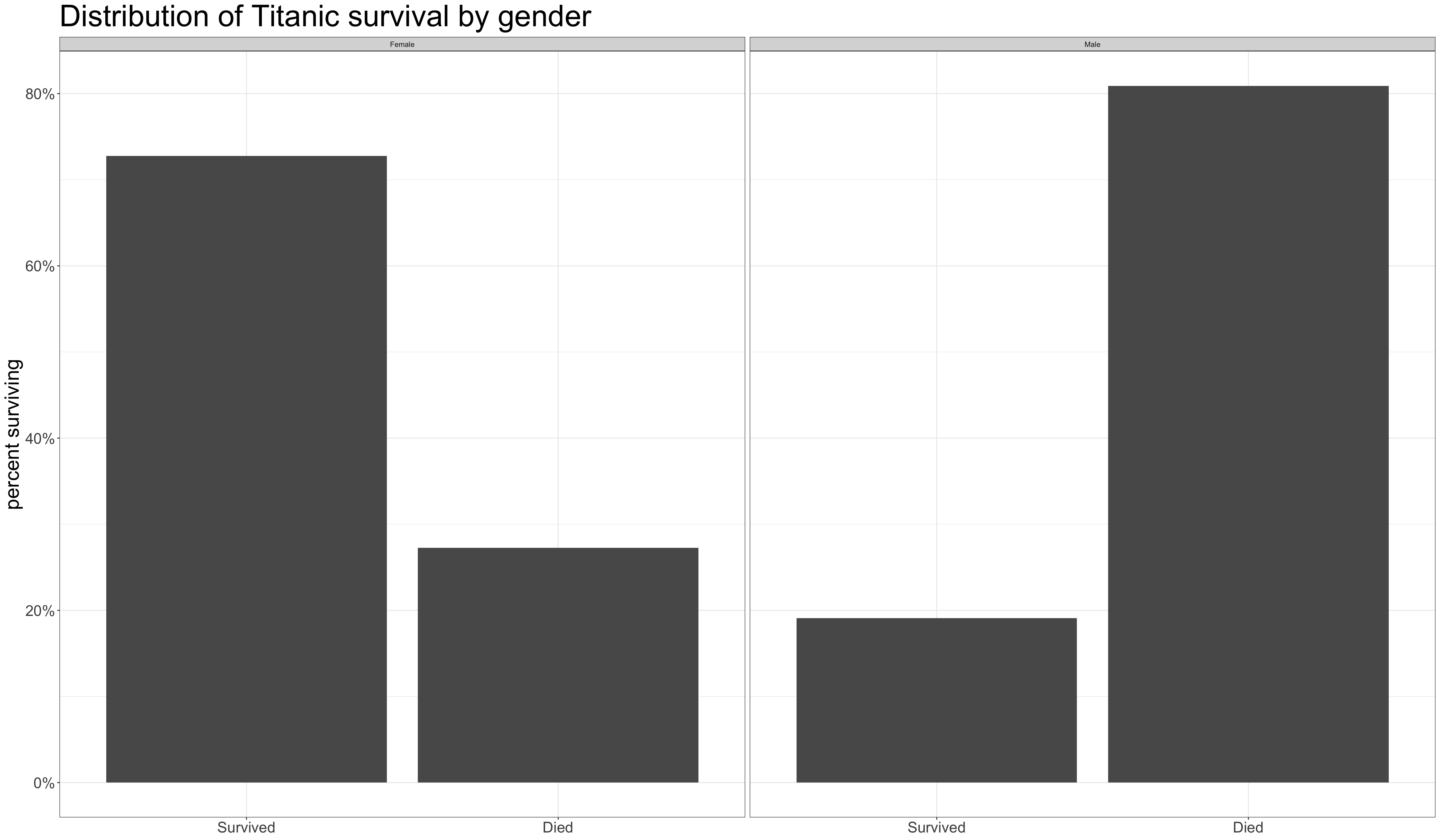
Code and output for comparative barplot

ggplot(titanic, aes(x=survival, y=..prop..,
                    group=1))+
  geom_bar()+
  scale_y_continuous(label=scales::percent)+
  labs(y="percent surviving", x=NULL,
       title="Distribution of Titanic survival by gender")+
  facet_wrap(~sex)+
  theme_bw()

The code here is identical to that for a simple barplot except for the addition of facet_wrap. The facet_wrap command allows us to make separate panels of the same graph across the categories of some other variable.

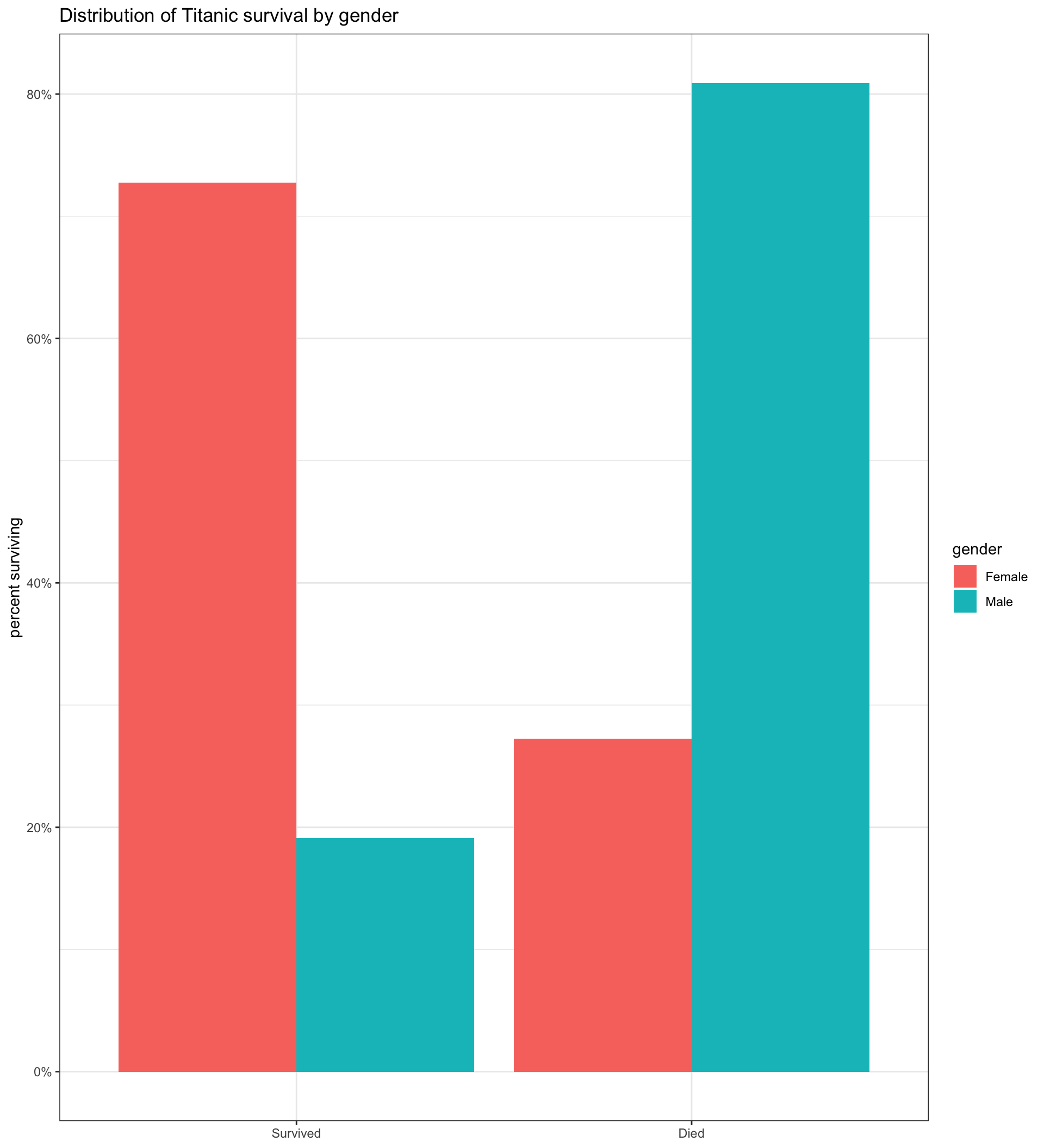
Comparative barplot by fill aesthetic

ggplot(titanic, aes(x=survival, y=..prop..,
                    group=sex, fill=sex))+
  geom_bar(position="dodge")+
  scale_y_continuous(label=scales::percent)+
  labs(y="percent surviving", x=NULL,
       title="Distribution of Titanic survival by gender",
       fill="gender")+
  theme_bw()

We group by sex and also add a fill aesthetic that will apply different colors by sex.

We add position="dodge" to geom_bar so that bars are drawn side-by-side rather than stacked.

We add fill="gender" to labs so that our legend has a nice title.

Presidential choice by education

# first command drops non-voters
temp <- droplevels(subset(politics, 
                          president!="No Vote")) 
tab <- table(temp$educ, temp$president)
# round and multiply prop.table by 100
# to get percents
props <- round(prop.table(tab, 1),3)*100
props
                     
                      Clinton Trump Other
  Less than HS           57.8  35.2   7.0
  High school diploma    42.8  51.7   5.5
  Some college           42.1  50.3   7.7
  Bachelors degree       46.4  44.1   9.5
  Graduate degree        65.0  30.4   4.5
ggplot(subset(politics, president!="No Vote"), 
       aes(x=president, y=..prop.., 
           group=educ, fill=educ))+
  geom_bar(position = "dodge")+
  labs(title="presidential choice by education",
       x=NULL,
       y="percent of education group",
       fill="education")+
  scale_y_continuous(label=scales::percent)+
  scale_fill_brewer(palette="YlGn") #<<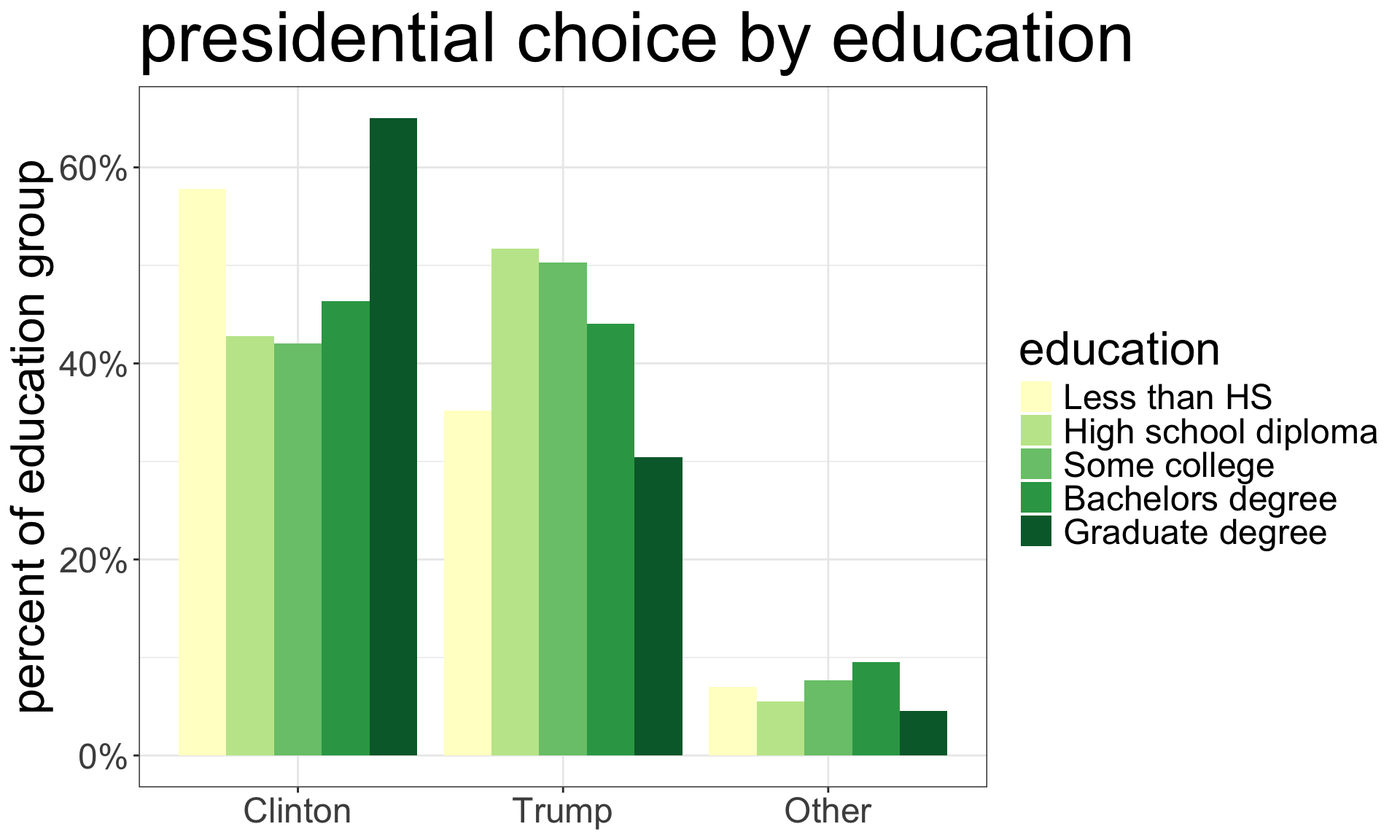

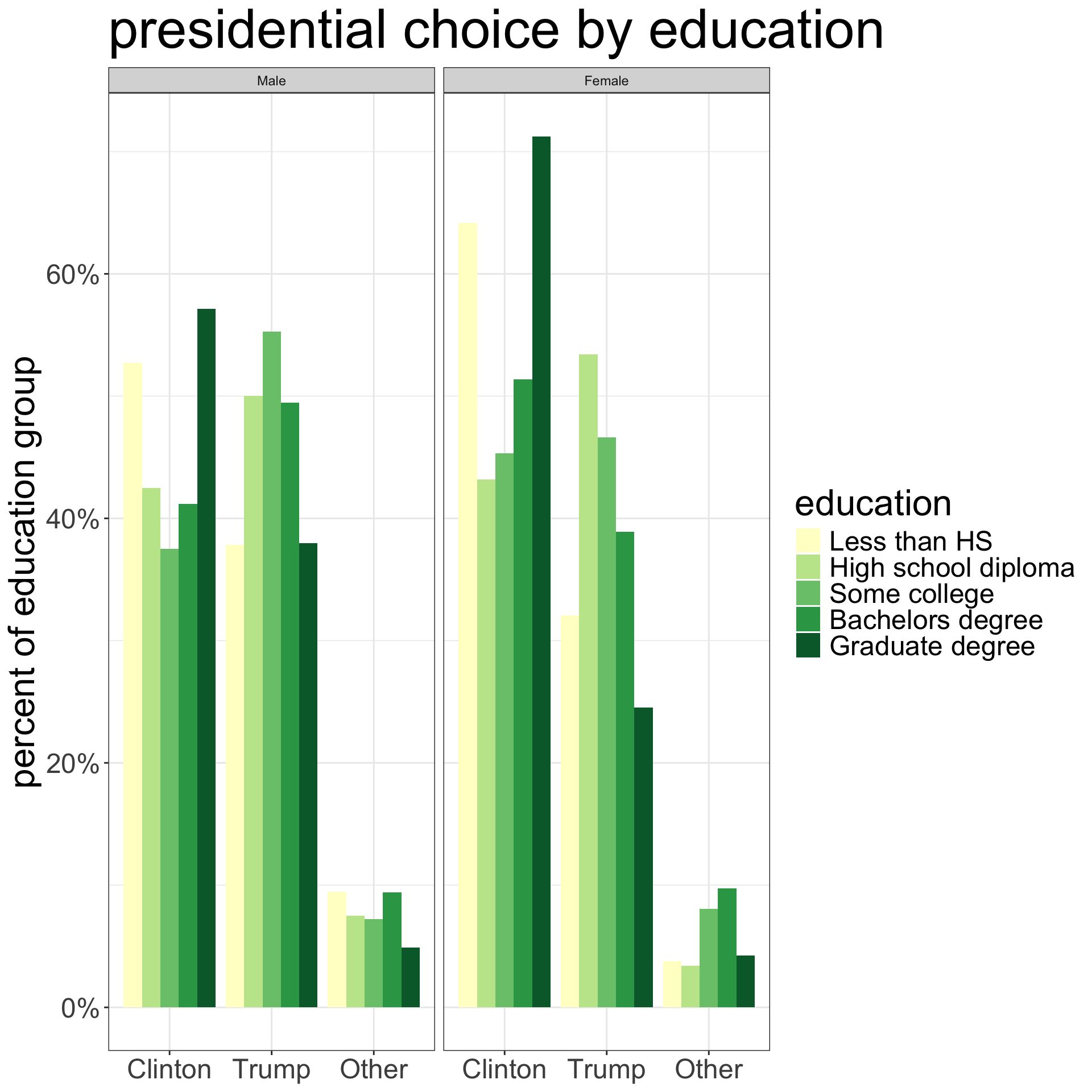
Super fancy three-way table

ggplot(subset(politics, president!="No Vote" &
                gender!="Other"), 
       aes(x=president, y=..prop.., 
           group=educ, fill=educ))+
  geom_bar(position = "dodge")+
  labs(title="presidential choice by education",
       x=NULL,
       y="percent of education group",
       fill="education")+
  scale_y_continuous(label=scales::percent)+
  scale_fill_brewer(palette="YlGn")+
  facet_wrap(~gender)

Just add a facet_wrap to see how education affected presidential voting differently for men and women.

How to compare differences in probabilities?

round(prop.table(table(titanic$sex, titanic$survival), 1)*100,2)
        
         Survived  Died
  Female    72.75 27.25
  Male      19.10 80.90

We could look at the difference (72.75-19.1=53.65), but this can be misleading because as the overall probability approaches either 0% or 100%, the difference must get smaller.

Titanic

38% of passengers survived

Costa Concordia

Roughly 99.2% of passengers survived

Calculate the odds

The odds is the ratio of “successes” to “failures.” Convert probabilities to odds by taking \[\texttt{Odds}=\texttt{probability}/(1-\texttt{probability})\]

Women

If 72.75% of women survived, then the odds of survival for women are \[0.7275/(1-0.7272)=2.67\]

About 2.67 women survived for every woman that died.

Men

If 19.1% of men survived, then the odds of survival for men are \[0.191/(1-0.191)=0.236\]

About 0.236 men survived for every man that died. Alternatively, 0.236 is close to 0.25, so about one man survived for every four that died.

Calculate the odds ratio

Odds ratio

To determine the difference in our odds we take the odds ratio by dividing one of the odds by the other.

\[\texttt{Odds ratio}=\frac{O_1}{O_2}=\frac{2.67}{0.236}=11.31\]

The odds of surviving the Titanic were 11.31 times higher for women than for men.

Cross-product method

Sex Survived Died
Female 339 127
Male 161 682

Multiply the diagonal bolded values together and divide by the product of the reverse-diagonal italicized values to get the same odds ratio.

\[\frac{339*682}{161*127}=11.31\]

Mean Differences

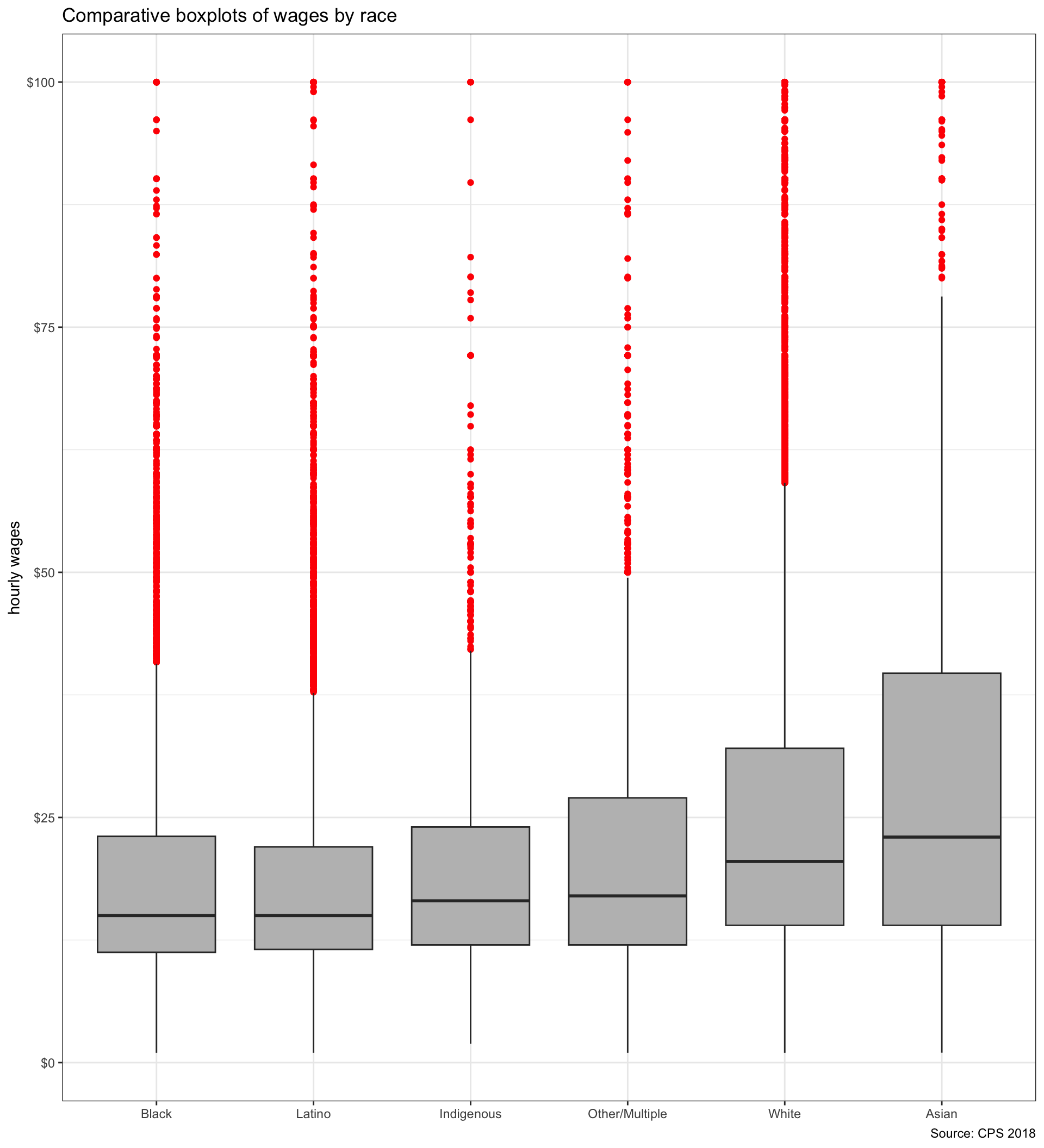
Comparative boxplots

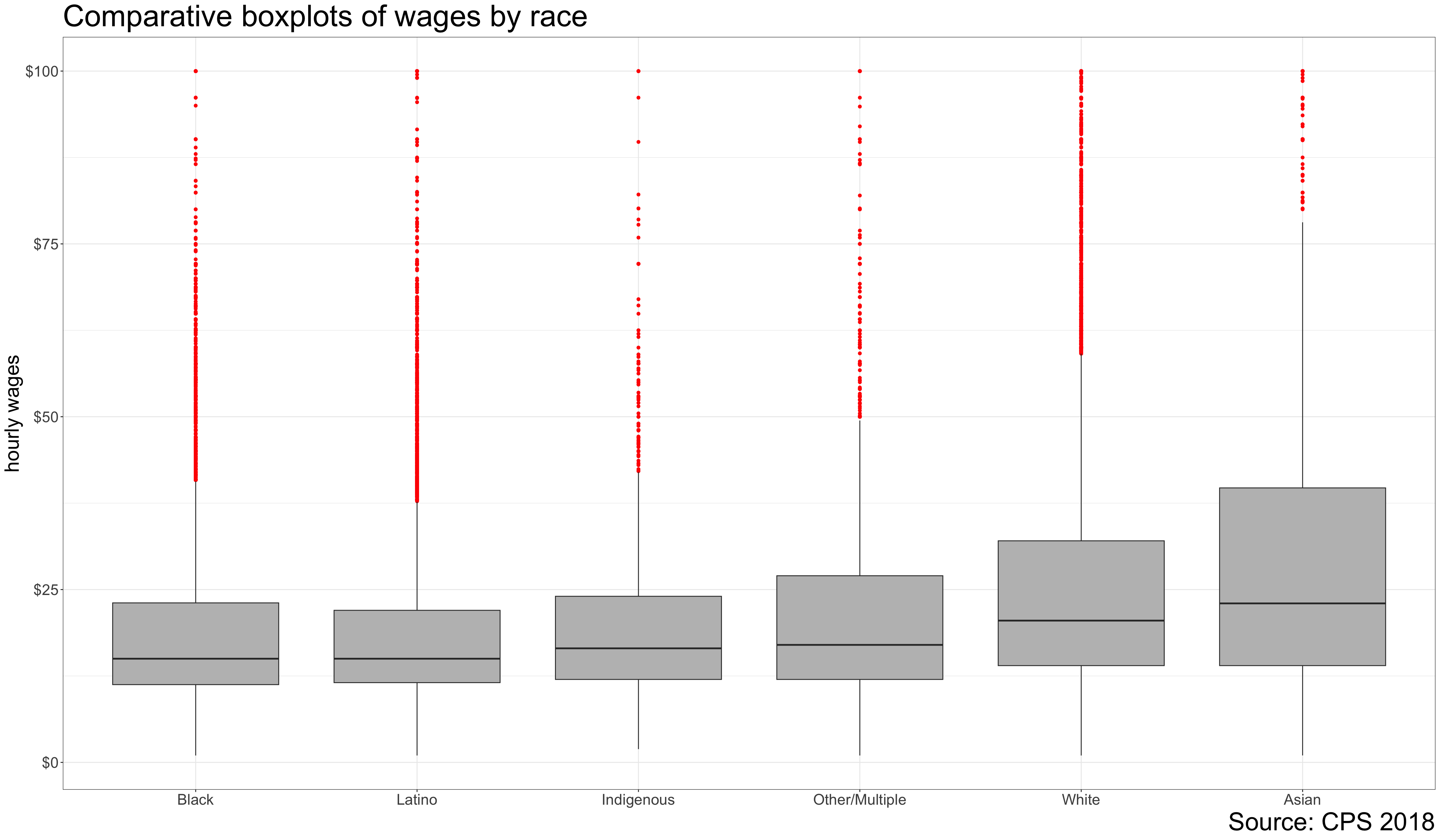
Code and output for comparative boxplot

ggplot(earnings, 
       aes(x=reorder(race, wages, median), #<<
           y=wages))+
  geom_boxplot(fill="grey", outlier.color="red")+
  scale_y_continuous(label=scales::dollar)+
  labs(x=NULL, y="hourly wages",
       title="Comparative boxplots of wages by race",
       caption="Source: CPS 2018")+
  theme_bw()

We just need to add an x aesthetic (in this case race) to the plot to get a comparative boxplot.

In this case, I have also used the reorder command to reorder my categories so they go from smallest to largest median wage by race. This is not necessary but will add more information to the boxplot.

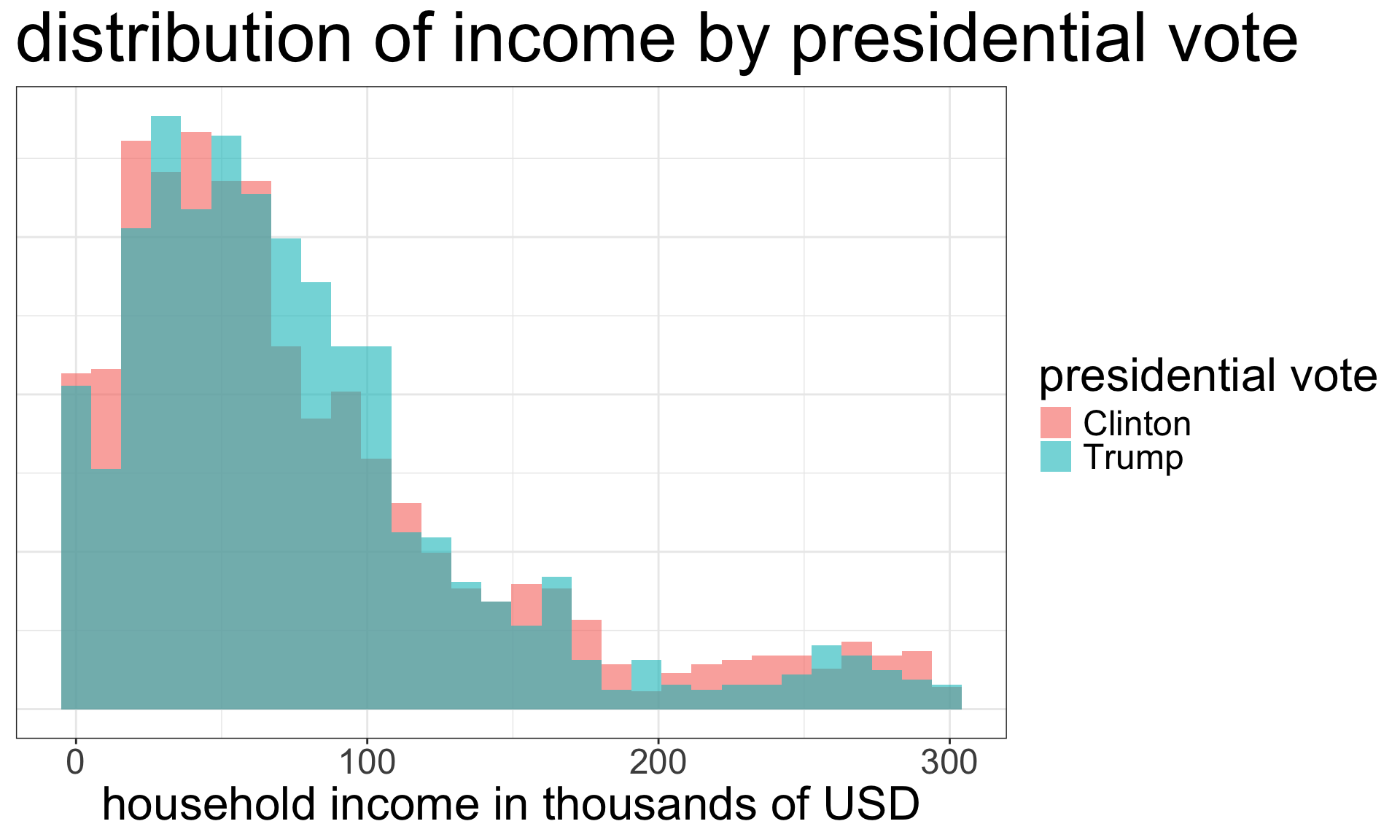
Income and presidential choice

Calculating mean differences

Use the tapply command to get the mean income of respondents separately by who they voted for:

tapply(politics$income, politics$president, mean)
 Clinton    Trump    Other  No Vote 
79.40396 77.37831 80.31188 60.69635
  • The first argument is the quantitative variable
  • The second argument is the categorical variable
  • The third argument is the function you want to run on the subsets of the quantitative variable

The mean difference is given by: \[80.23-77.33=2.9\] Clinton voters had a household income $2900 higher than Trump voters, on average.

What about median differences?

tapply(politics$income, politics$president, median)
Clinton   Trump   Other No Vote 
   61.0    64.0    68.5    44.0

Clinton voters had median household incomes $2000 lower than Trump voters. Why are the results different between the mean and median?

The income distribution of Clinton supporters is more right-skewed than Trump supporters so it has a higher mean but lower median. However, the differences are relatively small regardless.

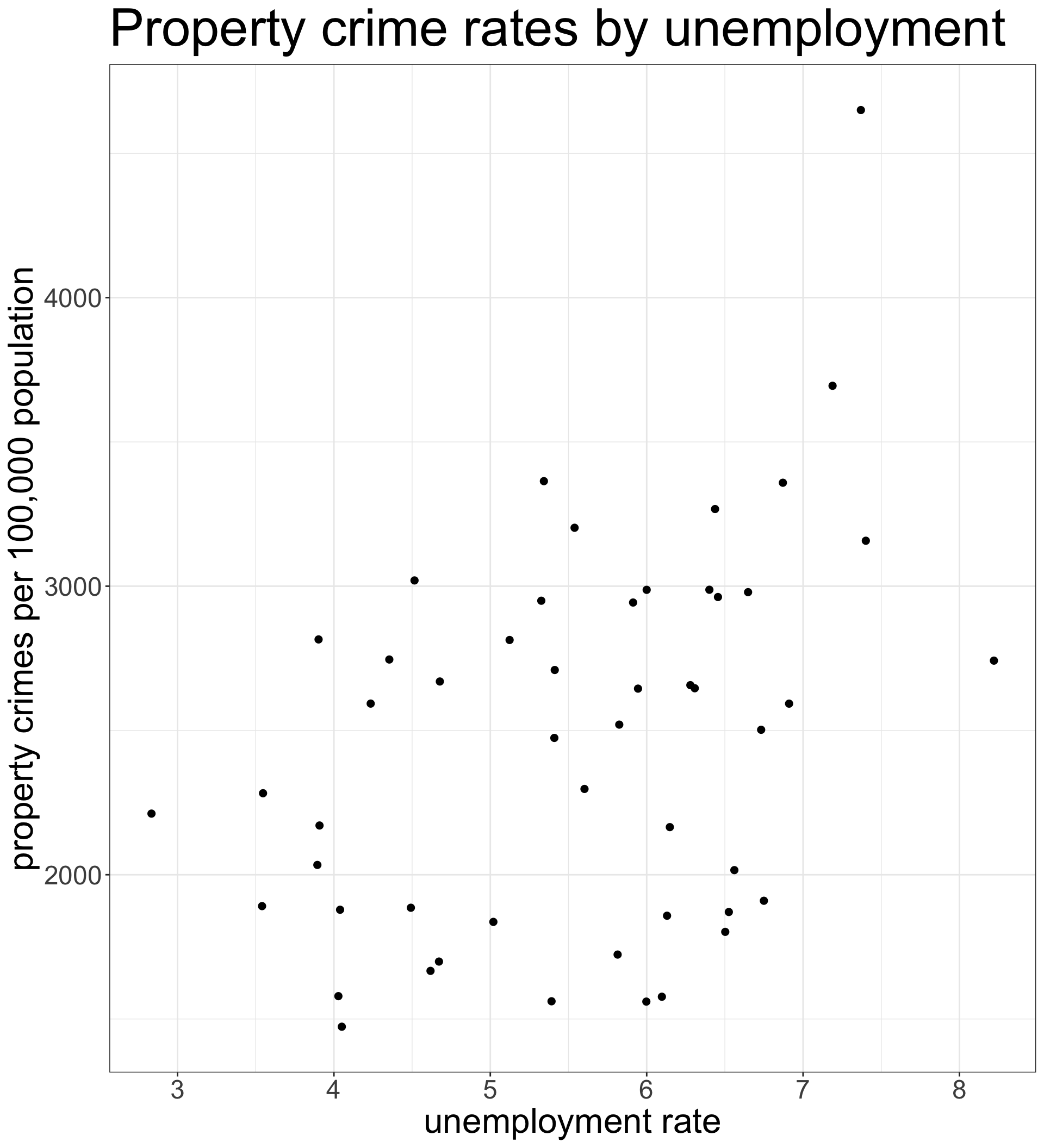
Scatterplot and Correlation Coefficient

Constructing a scatterplot

Constructing a scatterplot

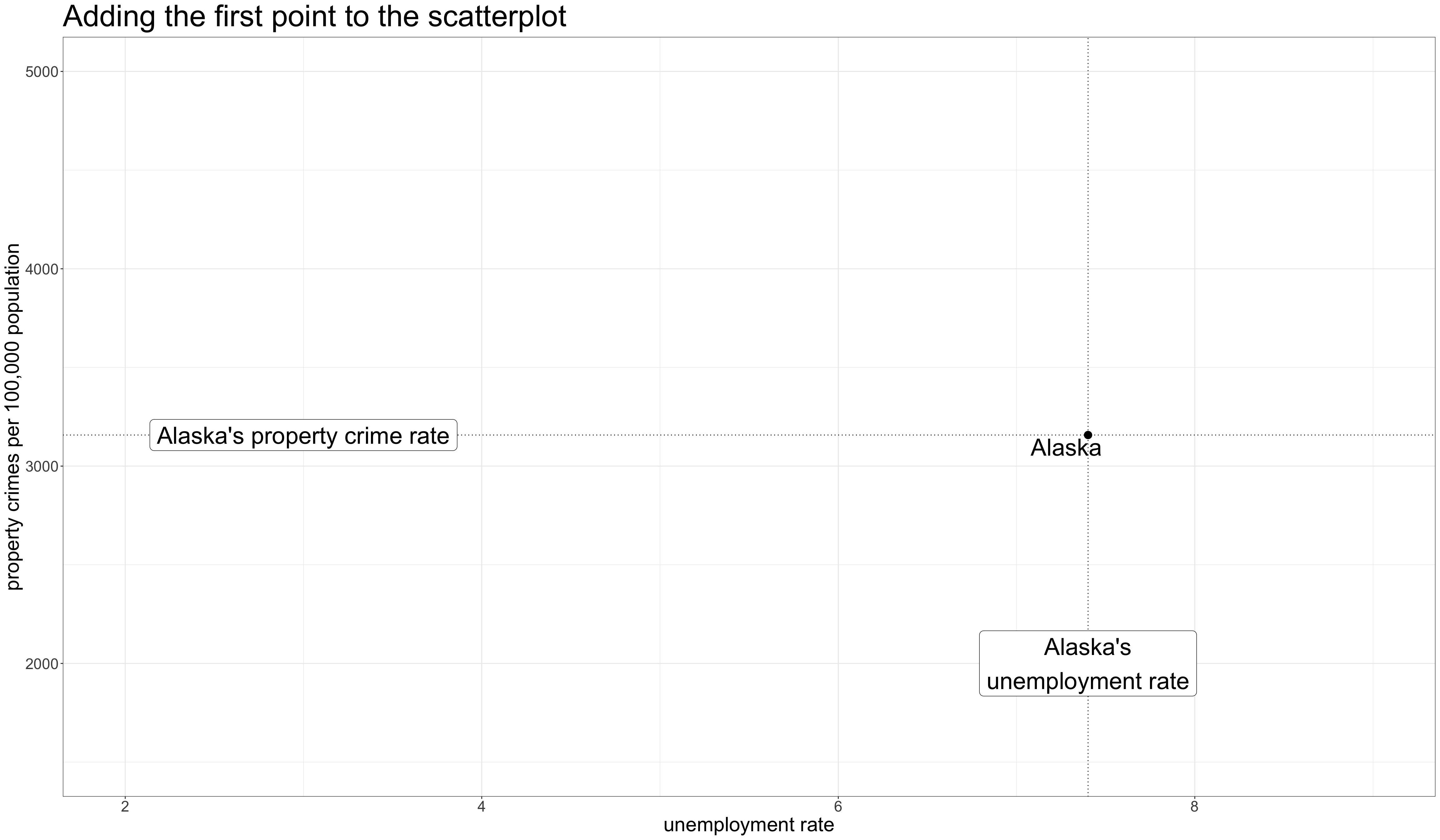
Constructing a scatterplot

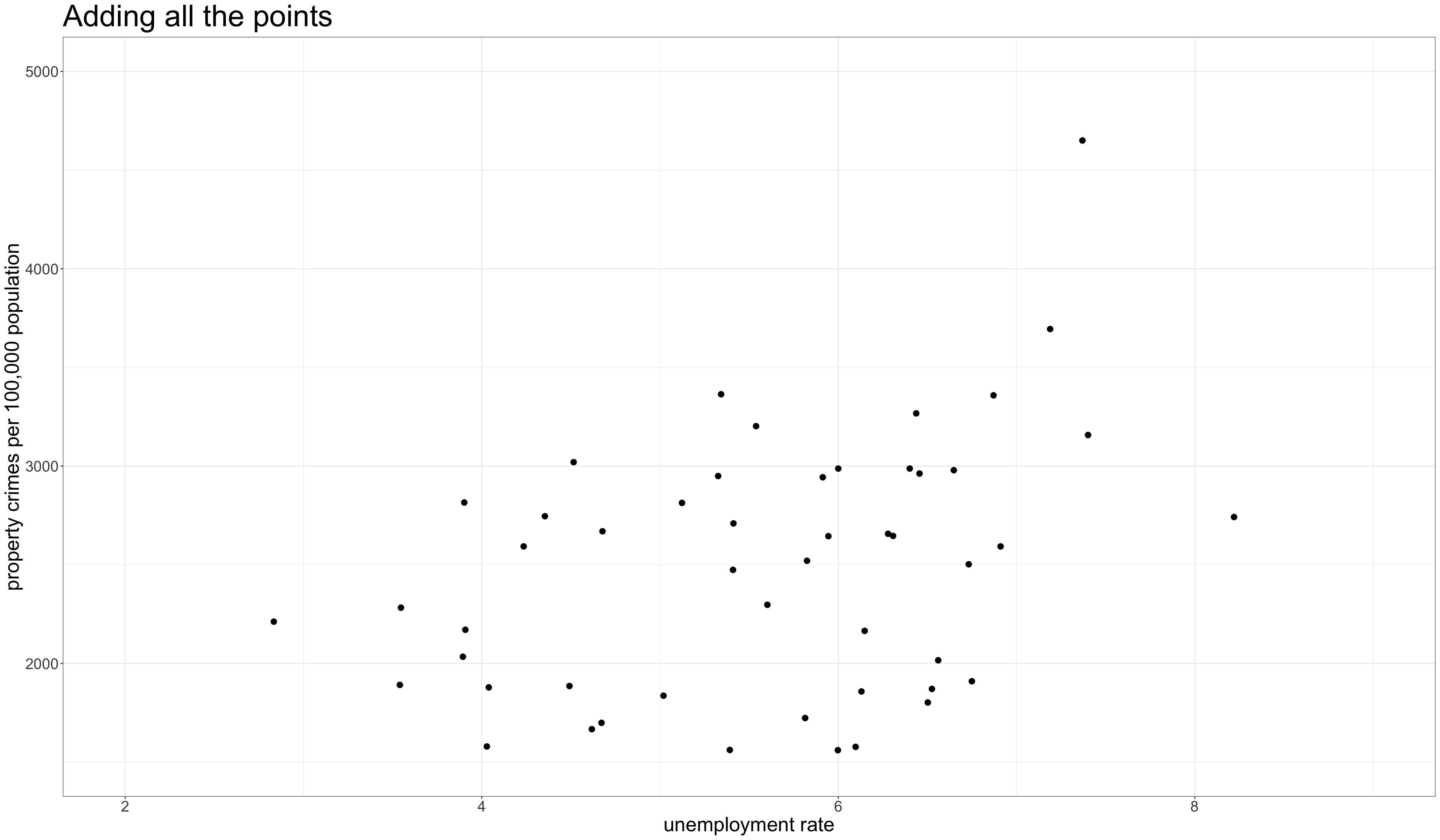
Code and output for scatterplot

ggplot(crimes, aes(x=unemploy_rate, y=property_rate))+
  geom_point()+
  labs(x="unemployment rate",
       y="property crimes per 100,000 population",
       title="Property crime rates by unemployment")

Define x and y variables in aesthetics.

Use geom_point to draw the points.

Use good labeling as always.

What are we looking for?

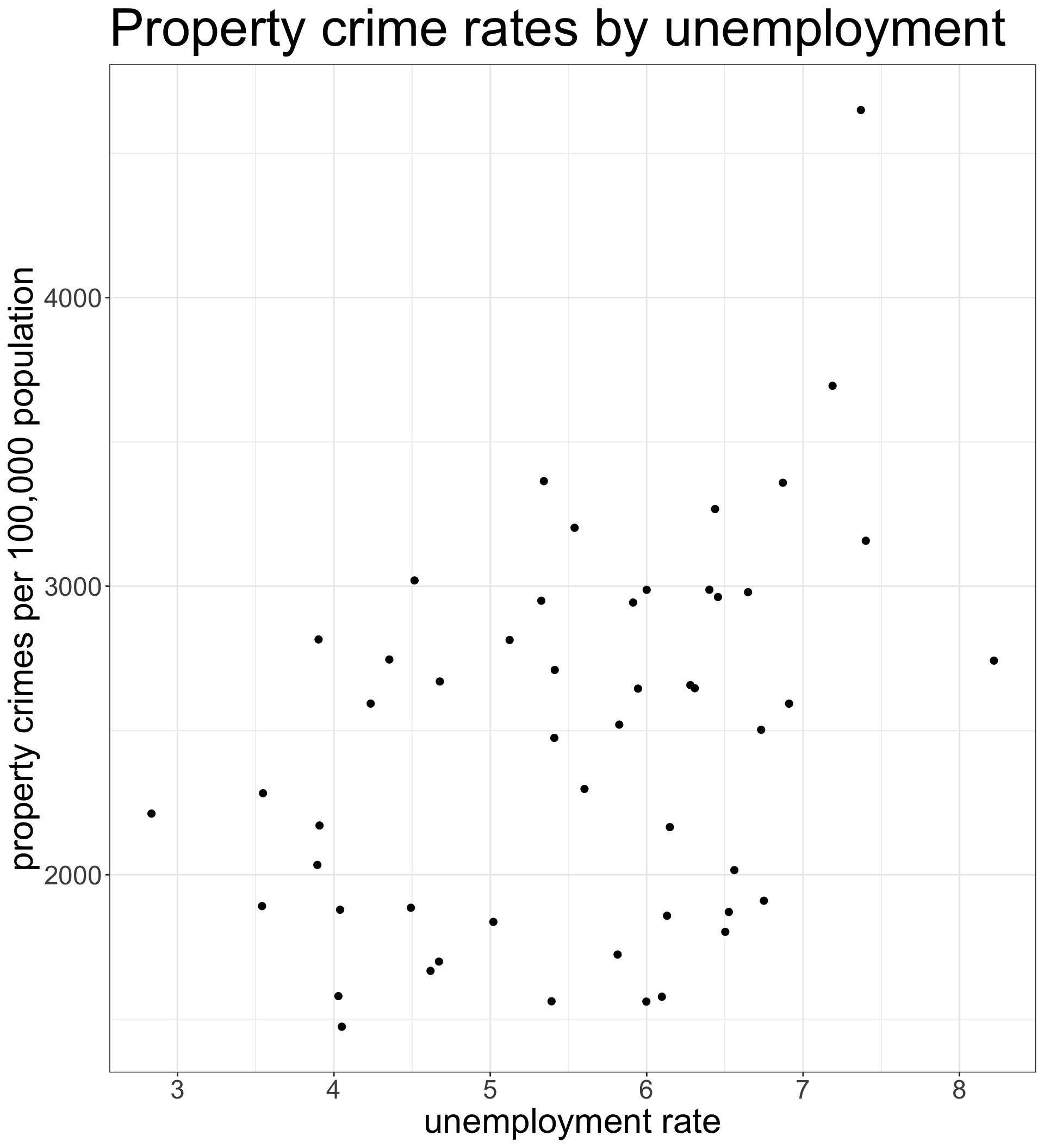
Direction
Is the relationship positive (y is high when x is high) or negative (y is low when x is high)?
Linearity
Does the relationship look linear or does it “curve?”
Strength
Do points fall in a broad cloud or a tight line?
Outliers
Are there outliers and are they inconsistent with the general trend?

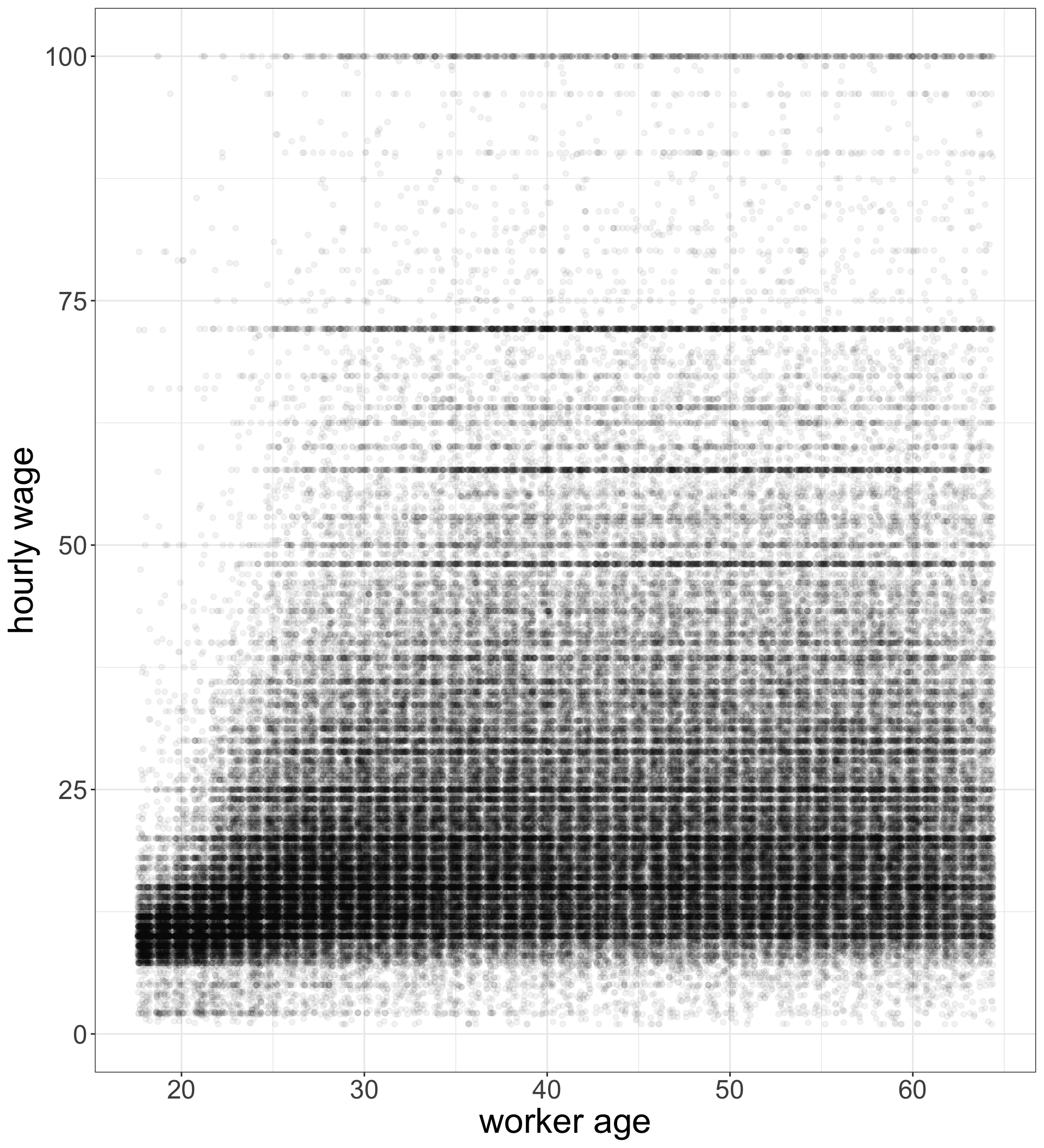
Overplotting with discrete variables

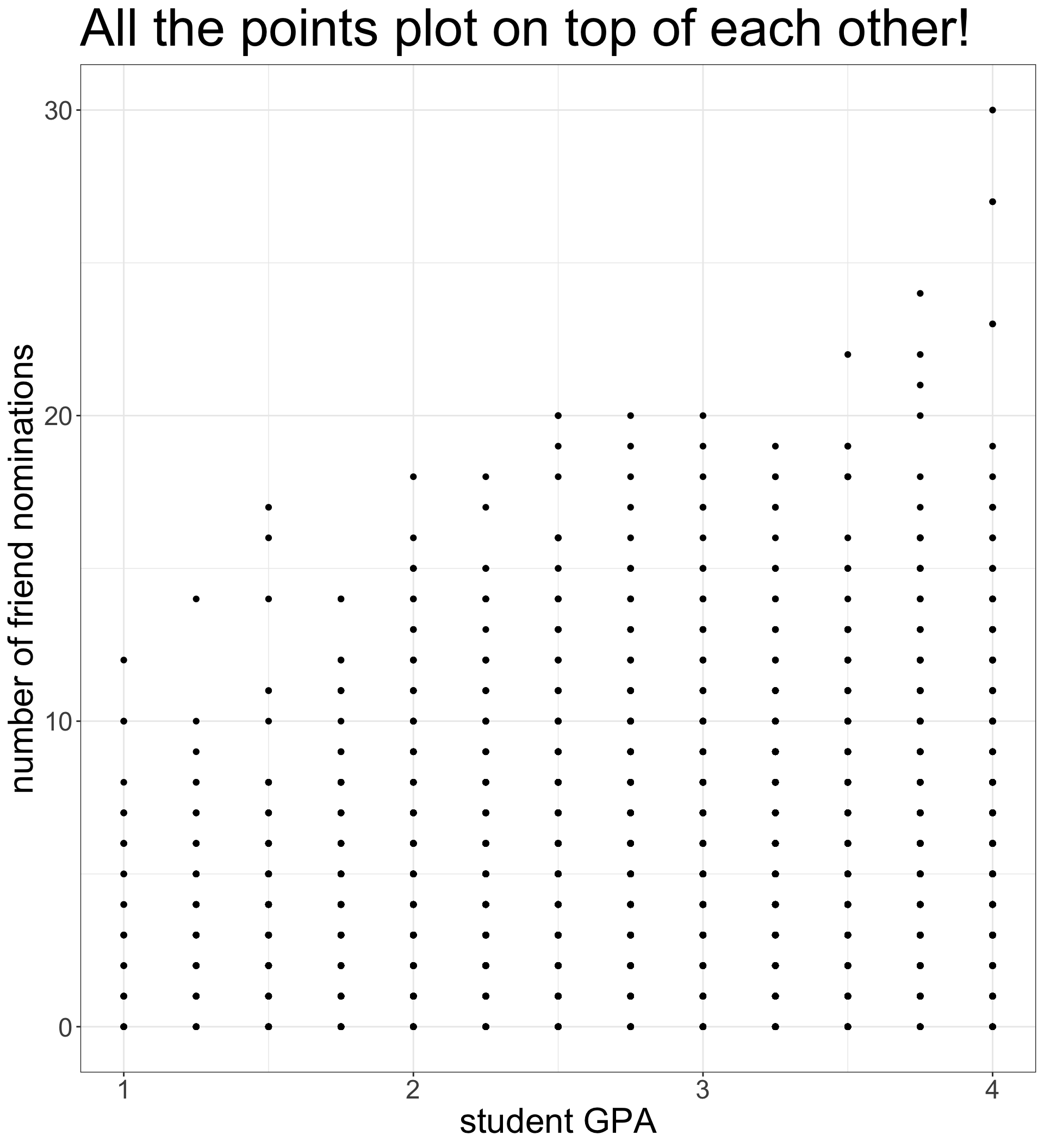
Overplotting corrections

ggplot(earnings, aes(x=age, y=wages))+
  geom_jitter(alpha=0.01, width=0.4)+
  labs(x="worker age",
       y="hourly wage")
  • geom_jitter instead of geom_point will add some randomness to x and y values so that points are not plotted on top of each other. The width and height arguments can be adjusted for more or less randomness (scale 0-1).
  • The alpha argument will create semi-transparent points (scale 0-1). I have it set very low because of the large number of points, but you should adjust as needed.

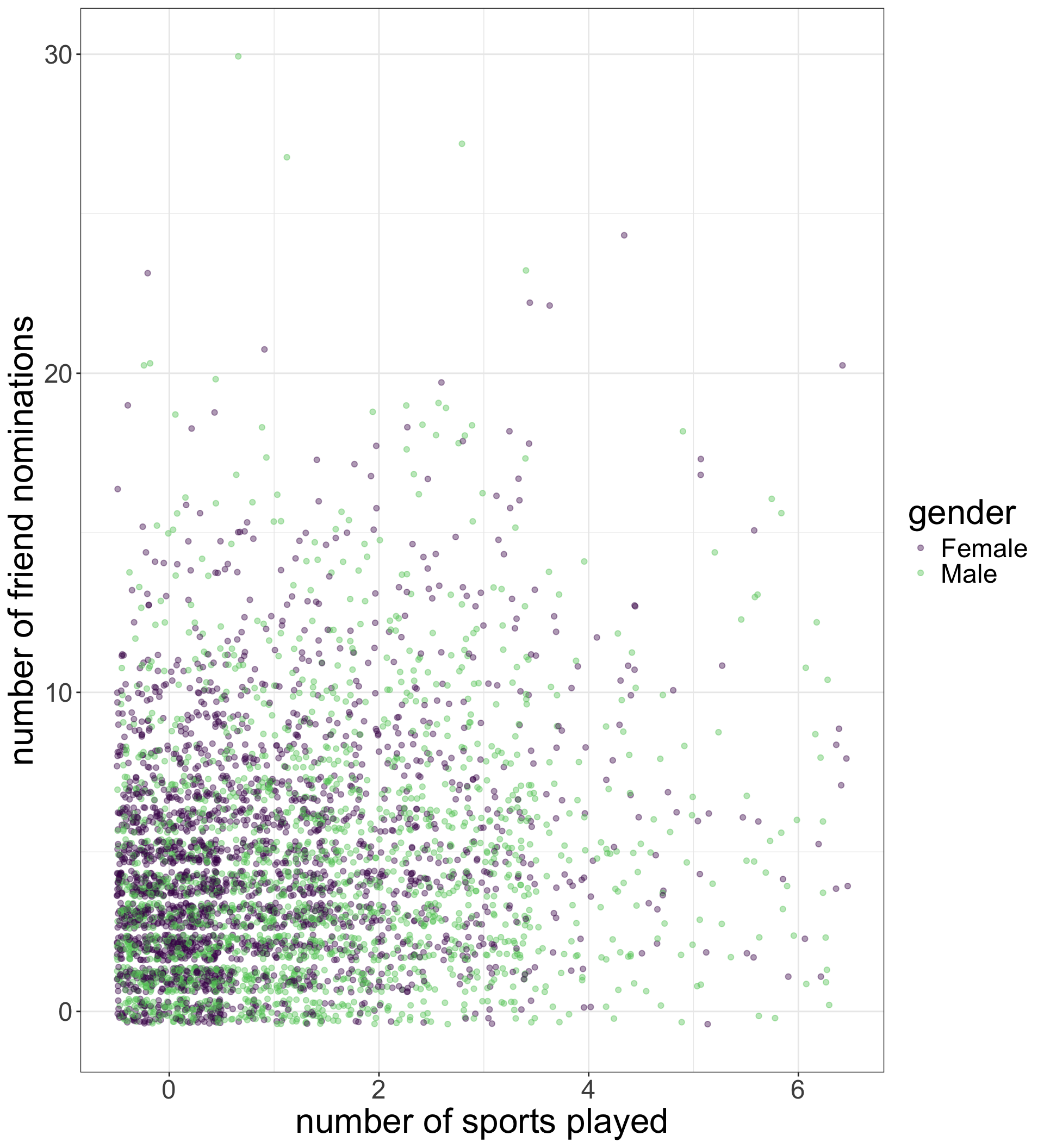
Adding a third variable by color

ggplot(popularity, aes(x=nsports, y=nominations,
                       color=gender))+
  geom_jitter(alpha=0.4, width=0.5, height=0.4)+
  scale_color_viridis_d(end = 0.75)+
  labs(x="number of sports played",
       y="number of friend nominations",
       color="gender")

I just add a third aesthetic to the aes command for color. This will color the points by the category of the variable used (in this case, gender).

I am using the viridis color scheme here, but you can adjust the palette if you like.

The correlation coefficient

The correlation coefficient (\(r\)) measures the association between two quantitative variables. The formula is:

\[r=\frac{1}{n-1}\sum^n_{i=1} (\frac{x_i-\bar{x}}{s_x}*\frac{y_i-\bar{y}}{s_y})\]

Let’s break it down

\((x_i-\bar{x})\) and \((y_i-\bar{y})\): Subtract the mean from each value of x and y to get distance above and below mean.

crimes$x_dist <- crimes$unemploy_rate-mean(crimes$unemploy_rate)
crimes$y_dist <- crimes$property_rate-mean(crimes$property_rate)

\((x_i-\bar{x})/s_x\) and \((y_i-\bar{y})/s_y\): Divide the difference by the standard deviation of \(x\) and \(y\). We now have the number of standard deviations above or below the mean.

crimes$x_sd <- crimes$x_dist/sd(crimes$unemploy_rate)
crimes$y_sd <- crimes$y_dist/sd(crimes$property_rate)

Evidence of positive or negative relationship

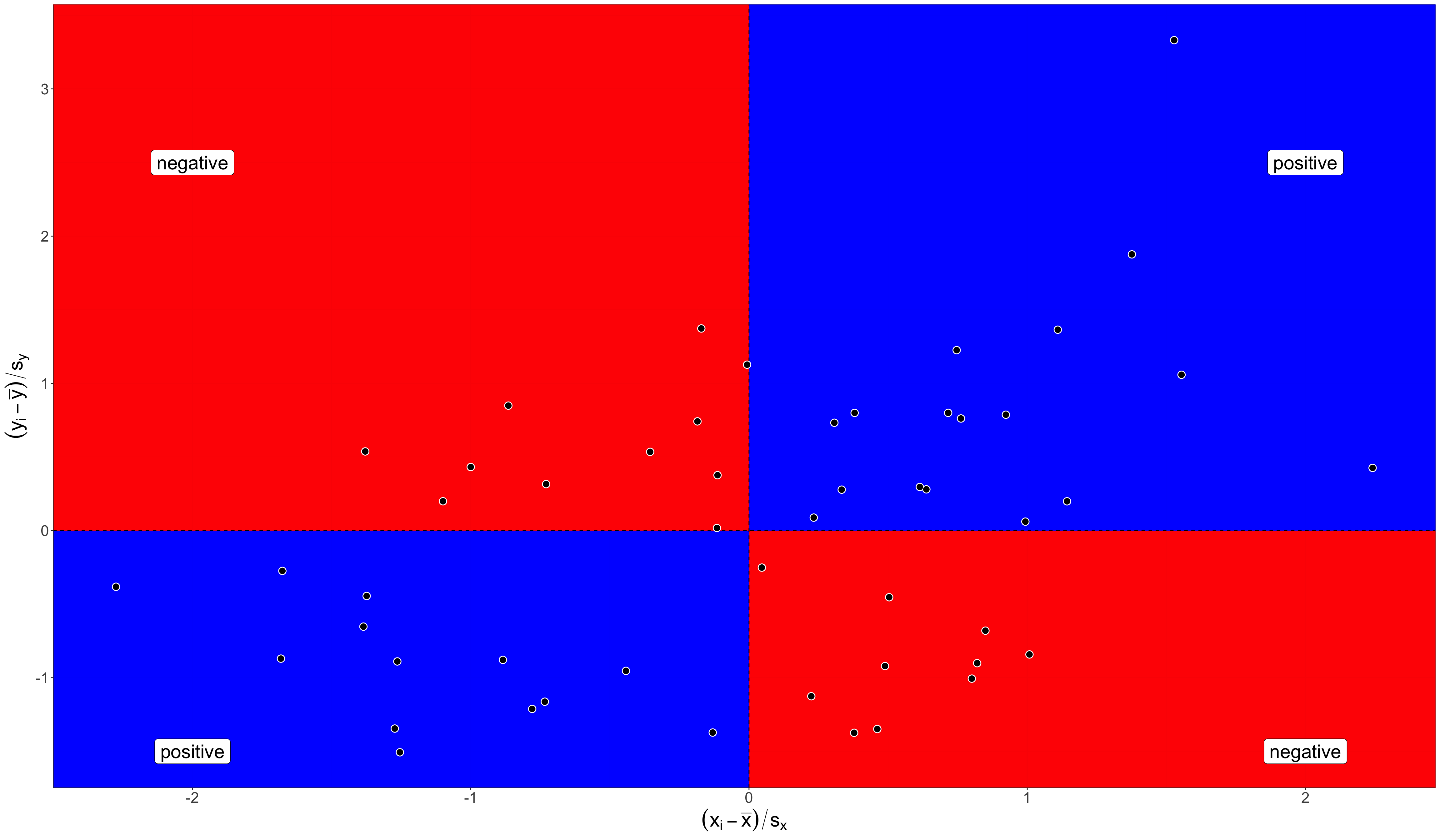
The correlation coefficient

\((\frac{x_i-\bar{x}}{s_x}*\frac{y_i-\bar{y}}{s_y})\): Multiply x and y values together. The results provides evidence of negative or positive relationship.

crimes$evidence <- crimes$x_sd*crimes$y_sd

\(\sum^n_{i=1} (\frac{x_i-\bar{x}}{s_x}*\frac{y_i-\bar{y}}{s_y})\): Sum up all the evidence, positive and negative.

sum_evidence <- sum(crimes$evidence)

\(\frac{1}{n-1}\sum^n_{i=1} (\frac{x_i-\bar{x}}{s_x}*\frac{y_i-\bar{y}}{s_y})\): Divide result by sample size to get final correlation coefficient.

sum_evidence/(nrow(crimes)-1)
[1] 0.4010458

Alternatively, use the cor command: 😎

cor(crimes$unemploy_rate, crimes$property_rate)
[1] 0.4010458

What does the correlation coefficient mean?

Direction
The sign of \(r\) indicates the direction of the relationship. Positive values indicate a positive relationship and negative values indicate a negative relationship. Zero indicates no relationship.
💪 Strength
The absolute value of \(r\) indicates the strength of the relationship. The maximum value of \(r\) is 1 and the minimum value is -1. You only reach these values if the points fall exactly on a straight line.
⚠️ Limitations
\(r\) is only applicable for linear relationships and \(r\) can be severely affected by outliers.

Simulated examples of correlation strength

Sociology 312/412/512, University of Oregon